E' ormai noto a tutti che la firma digitale è il risultato di un procedimento crittografico, ma non sempre sono chiari i rapporti tra crittografia e firma digitale. Cerchiamo di capire come si passa dalle tecniche per rendere segreto un documento alla certezza dell'autenticità e dell'integrità del medesimo.

2.1. Un "baco" della matematica

La crittografia, cioè la scienza che studia i sistemi per rendere certe informazioni segrete e leggibili solo a chi possiede la chiave per decifrarle, oggi è fondata quasi esclusivamente sull'impiego di sistemi informatici e di programmi che svolgono complesse operazioni matematiche.
I sistemi crittografici attuali (e, tra essi, quelli che qui ci interessano) sono fondati su una "lacuna" della scienza matematica: non esiste un sistema veloce per calcolare i fattori primi (cioè i numeri indivisibili) che, moltiplicati fra loro, formano un numero. E' necessario eseguire una per una tutte le divisioni per scoprire se un certo numero è divisibile per un altro senza che ci sia un "resto". Se il numero da analizzare è molto grande, nell'ordine delle centinaia di cifre, occorre un tempo lunghissimo.

Ora, se trasformiamo in numeri tutte le lettere che compongono un testo e poi compiamo su questi numeri una serie di moltiplicazioni, otteniamo un numero molto grande. Chi è a conoscenza delle operazioni compiute e dei valori per i quali sono stati moltiplicati i numeri di partenza - cioè chi dispone del cifrario¹ e della chiave - è in grado di decifrare il contenuto. Chi non dispone di queste informazioni, deve cercare di rompere il cifrario per decrittare il testo. E per questo non può che ricorrere alla forza bruta di un calcolatore, che provi, una dopo l'altra, tutte le combinazioni possibili. Se il numero è abbastanza grande e il cifrario è abbastanza complicato, anche un calcolatore di enorme potenza può impiegare un tempo molto lungo, misurabile in anni, o addirittura in secoli, per trovare la chiave e mettere in chiaro il testo cifrato.

Dunque la sicurezza della crittografia non è una sicurezza assoluta, ma relativa al tempo necessario per rompere il cifrario. Più il cifrario è complesso, più tempo occorre per venirne a capo, a parità di potenza del sistema di elaborazione. In termini tecnici si parla di robustezza del sistema di crittografia e in genere si fa riferimento alla lunghezza della chiave di cifratura: più essa è lunga, più il cifrario è robusto.

2.2. La crittografia a chiave simmetrica

Immaginiamo di sostituire un numero a ogni carattere che compone un testo (testo chiaro), e poi di compiere una serie di moltiplicazioni su questi numeri. Alla fine viene fuori un numero molto grande (testo cifrato). Il cifrario consiste nei fattori che sono stati usati per le moltiplicazioni e nelle diverse fasi dell'operazione (moltiplicazioni di singole parti, spostamenti e altri accorgimenti che "rimescolano" i dati).
Chi dispone del cifrario può compiere tutti i passaggi in senso inverso e ricostruire il testo chiaro, come mostra lo schema seguente.

Fig. 1. Cifrario simmetrico

In questo caso la stessa chiave serve per cifrare e decifrare il testo

Questo tipo di cifrario ha un grave difetto: se la chiave viene a conoscenza di chi è interessato a conoscere abusivamente il contenuto del testo, la segretezza viene meno. Occorre un canale sicuro per trasmettere preventivamente la chiave al destinatario. Ma se si dispone di un canale veramente sicuro, tanto vale usarlo per trasmettere direttamente il testo!
Inoltre è sconsigliato usare la stessa chiave per inviare messaggi segreti a più destinatari: maggiore è il numero di persone a conoscenza del cifrario, più alto è il rischio che la segretezza venga meno.
Dunque, se si deve comunicare in via riservata con più persone, è necessario disporre di tante chiavi quanti sono gli interlocutori (meno uno): è facile se gli interlocutori sono pochi, ma sempre più difficile da gestire a mano a mano che il loro numero aumenta.

Per ovviare a questi inconvenienti, fin dagli anni '70 è stata messa a punto una nuova generazione di cifrari, detti "a chiave asimmetrica" o (tra poco vedremo perché) "a chiave pubblica".

2.3 La crittografia a chiave asimmetrica (o a chiave pubblica)

Nella crittografia a chiave pubblica si impiegano cifrari che fanno uso di due chiavi diverse, univocamente correlate: una serve a cifrare il testo chiaro, una decifrare il testo cifrato con la prima (non importa quale delle due chiavi della coppia venga usata per la prima operazione). I punti fondamentali sono tre:

1. non si può decifrare il testo con la stessa chiave usata per cifrarlo
2. le due chiavi sono generate con la stessa procedura e correlate univocamente;
3. conoscendo una delle due chiavi, non c'è nessun modo di ricostruire l'altra.

Ecco come funziona il procedimento:

Fig. 2. Cifrario asimmetrico

Cifratura e decifratura di un documento con un cifrario a chiave asimmetrica

2.4 Informazioni segrete con cifratura asimmetrica

Questo sistema offre una straordinaria possibilità: chiunque può inviare un messaggio segreto a chi renda pubblica una delle due chiavi. La cosa funziona in questo modo:

1. chi intende usare un sistema crittografico a chiave pubblica, deve munirsi di un software crittografico (compatibile con quelli usati dagli altri interessati) e generare, al riparo da occhi indiscreti, la propria coppia di chiavi;
2. quindi deve rendere disponibile a chiunque una delle due chiavi (chiave pubblica), mentre deve custodire gelosamente l'altra (chiave privata);
3. per mandare a qualcuno un messaggio segreto, deve cifrarlo con la chiave pubblica del destinatario;
4. solo il destinatario può decifrare il messaggio, perché solo lui dispone della chiave privata correlata alla chiave pubblica usata dal mittente.

Schematicamente, la procedura è questa:

Fig. 3. Invio di un messaggio cifrato con un sistema asimmetrico

Il mittente cifra il testo con la chiave pubblica del destinatario, questi lo decifra con la propria chiave privata

Naturalmente è indispensabile che la chiave privata venga mantenuta assolutamente segreta, altrimenti tutto il sistema va a rotoli.

2.5. Il riconoscimento del mittente

I cifrari a chiave pubblica possono essere usati anche "al contrario", cioè cifrando il testo chiaro con la chiave privata del mittente. A prima vista questa operazione non serve a nulla, perché chiunque può decifrare il testo con la chiave pubblica dello stesso mittente. Invece è una funzione importantissima, perché, se l'operazione riesce, significa che il messaggio è stato inviato proprio dal titolare della chiave pubblica usata per la decifratura, perché solo lui dispone della chiave privata con la quale il testo è stato cifrato. Ecco il semplice schema della procedura:

Fig. 4. Testo cifrato con la chiave privata del mittente

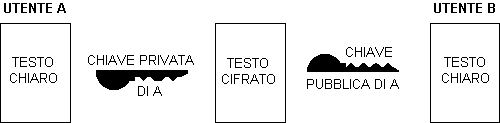
Se B riesce a decifrare il messaggio con la chiave pubblica di A, questi è certamente l'autore del testo

E' possibile anche combinare le due operazioni: il mittente può inviare un messaggio segreto, cifrato con la propria chiave privata e con la chiave pubblica del destinatario. Questi decifra il messaggio con la propria chiave privata e con la chiave pubblica del mittente. In questo modo si ottiene sia la segretezza del testo, sia la certezza (relativa, come vedremo tra un attimo) dell'identità del mittente.
Questa possibilità è di scarso rilievo nel discorso sul documento informatico e quindi non ce ne occupiamo in questa sede.

2.6 La firma digitale

A questo punto siamo pronti a capire come funziona la firma digitale, cioè come si può dare a un testo chiaro la certezza dell'identità del firmatario e dell'integrità del contenuto.
Il sistema più elementare è inviare un testo chiaro insieme a una versione cifrata con la chiave pubblica del mittente. Si opera sul testo cifrato con la chiave pubblica del mittente e, se i due testi risultano uguali, si ottengono le due certezze sull'identità del mittente e sull'integrità del contenuto.

Tuttavia questo sistema è lento, perché è necessario cifrare e decifrare tutto il testo, che potrebbe essere molto lungo. Si ricorre allora a una scorciatoia, che consiste nel cifrare solo un brevissimo riassunto del testo stesso, ottenuto con una procedura detta funzione di hash: pochi caratteri che costituiscono l'impronta del testo. Se, alla fine della procedura, l'impronta che risulta dalla decifratura è uguale a quella che si ottiene applicando la funzione di hash al testo chiaro, vuol dire che esso non è stato alterato dopo la generazione della firma digitale.
La cosa può apparire complicata, ma in pratica basta fare clic su un pulsante e il computer in pochi istanti fornisce la risposta (in uno dei prossimi articoli vedremo qualche esempio di generazione e verifica della firma digitale)

Vediamo anche questo schema:

Fig. 5. Generazione e verifica della firma digitale

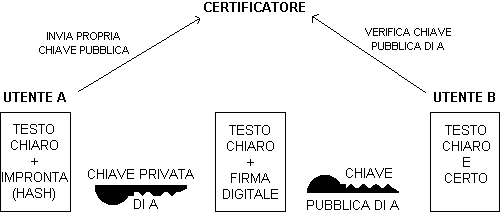
La firma digitale si genera applicando la propria chiave privata all'impronta del testo

Qui abbiamo introdotto una figura nuova: è quella del certificatore, cioè di un soggetto che attesta che la chiave pubblica di A appartiene effettivamente ad A e non a un altra persona.
E' chiaro che la certificazione della chiave pubblica costituisce il punto critico di tutto il sistema, perché, in assenza di controlli rigorosi, non ci vuole molto a rendere pubblica una chiave attribuendola a un altro titolare e compiere così qualsiasi atto illecito sotto false generalità.

Al certificatore sarà dedicata la prossima puntata di questa introduzione alla firma digitale.

----------------------

¹ Introduciamo in neretto i termini tecnici della crittografia. Un piccolo glossario sarà pubblicato su uno dei prossimi numeri di InterLex